This page was last updated on 1 January 1998.

Triplanetary Map Variants and Ideas

Contents

Pocket Triplanetary

Build-your-own Triplanetary board

Triplanetary gravity variants

Pocket Triplanetary

Introduction

One of the neat things about Triplanetary is that the all that's really necessary for play are the laminated map and colored markers; the map can be recreated on 8.5" x 11" paper, allowing the game to be extremely portable and playable in tight places.

Necessary materials

  • 8.5" x 11" hex paper, with 1/4 inch hexes (such as The Armory's "A" Hex & Graph Paper).

  • Triplanetary map (as a guide). [Note: All measurements assume the second edition Triplanetary map, although this will work with the first edition map as well.]

  • Sheet protectors, or access to a lamination machine.

Procedure

This is actually fairly simple. The second edition Triplanetary map is 35 x 51 hexes, short-grained (i.e., the rows are parallel to the short side of the map). The toughest part of this project was finding short-grained hex paper of the right size. The Armory hex sheets mentioned above are 34 x 51 hexes, short-grained, and I decided that was close enough.

Simply transpose the features from the Triplanetary map to the smaller hex sheet. (Gravity arrows are somewhat problematic; I simply drew the half-gravity arrows with short tails, and the full-gravity arrows with long tails.) I recommend photocopying the resulting map several times, which will allow you to store multiple in-progress games. After that, I used highlighters to mark the major objects, although this is not necessary. For the asteroid belt, I recommend lightly shading the hexes -- it shows up better than dotes, and is a lot less tedious. (Remember that the asteroid field near Clandestine is particular dense -- I used a blue highlighter to mark those hexes.) Finally, I laminated the maps. [Click here to see the map before photocopying.]

Build-your-own Triplanetary board

Introduction

With a large vinyl hexmat and some homemade adhesive-backed solar system geography, it is possible to create your own one-use Triplanetary maps.

Necessary materials

  • Large vinyl hexmat, such as Chessex's "Megamat #9762 16mm Numbered w/LOS Dots".

  • 8.5" x 11" hex paper with the same size hexes as the hexmat.

  • Avery #5165 or equivalent 1 x 1 labels (i.e., each 8.5" x 11" page consists of 1 label).

  • Access to a laminating machine.

  • Exacto knife.

Procedure

  1. Using a plastic template I bought at a local stationary store (Staedtler Pocket General Purpose Professional Template), I filled the sheet with a wide variety of gravity wells, including some with experimental double-arrows and others that were obviously components of binary star systems. (Note that I did not add the circles representing the planets/stars nor fill in the gravity arrows at this time -- that comes later.)

  2. I then photocopied the sheet, giving me a sufficient supply for the foreseeable future. [Click here to download the sheet.]

  3. Next I added circles of different sizes representing planets and filling in some of the gravity arrows (see my gravity variant ideas below), and added dots representing asteroid fields to some of the leftover hexes.

  4. After photocopying the sheet onto a single Avery #5165 label, I slit a lamination pocket in half and laminated the front of the sheet.

  5. Finally, using an Exacto knife, I cut the resulting laminated label into its constituent geographical features.

I now have a set of a set of Triplanetary geography with an adhesive backing for use on my vinyl hex mat.

Note:
  • While I have not tested this theory, I suspect that it would not be good to leave the stickers on the map for a long time. I always make sure they are removed after the game is over, and no problems have yet resulted.

  • The lamination has a tendency to cause the stickers to curl up. I find that putting the stickers in an envelope is sufficient to keep them relatively flat. After they are applied, the adhesive is sufficient to keep them in place.

Triplanetary gravity variants

There are two specific classes of gravity variations that I want to mention. They can be used together if so desired.

Optional gravity

The scale of the Triplanetary map is a funny thing -- anyone who tries to calculate the size of a Triplanetary map hex based on the distance between the various planets will discover many quirks (read "inaccuracies") in the map, of which here are a few:
  • The areas in space represented by the hexes on the map are not constant in size;
  • Gravity extends much farther away from the source on the map than it does in the Real World (tm);
  • Planets are way too big;
  • The Moon orbits the Earth at 20 million miles or so.
Of all of these points, I think that the second one -- gravitational effects extending too far -- is potentially the most troublesome, because it's the only one that can't be solved simply by recreating the map in the proper scale.

I think I have come up with a tentative solution, although it will change the character of the game a bit: simply treat all gravity arrows (except those around the Sun) as optional. Gravity arrows thus represent not a gravity well which affects the entire hex, but a gravity well close enough that the ship could maneuver into it by expending thrust at a level below the granualarity of the thrust system.

This idea came to me as I was working on a variant of Triplanetary to use as a tactical module for fighting battles based on the Company War timeperiod of C. J. Cherryh's Alliance-Union books. Spacecraft in this timeperiod are much more powerful than your standard Triplanetary ship in terms of engine performance (weaponry, too, but that's another matter entirely); as a result, it's simply inconceivable that a combat vessel would go careening off into space because of a gravity arrow, but a shrewd captain may use the gravity of a planet to perform a maneuver otherwise outside a ship's performance envelope. Also, planets and such are important because they are obstacles to hide behind, and because they potentially can affect a ship's jump drive.

This rule does beg some interesting questions, e.g., can ships now break orbit without expending thrust? How are the hollow gravity arrows handled? How are unpiloted objects (mines and torpedoes) handled? I haven't thought through all these ramifications yet.

New types of gravity hexes

In Triplanetary, there are two types of gravity hexes: full gravity, which cause the head of a ship's vector arrow to be pushed one hex in the direction of the filled-in arrow for every hex passed through, and light gravity, which cause (depending on which edition you are playing) the head of a ship's vector arrow to be pushed one hex in the direction of the arrow for either every other outlined arrow or one out of every two outlined arrows passed through. I have been experimenting with some other types of gravity hexes, to take into account some other types of stellar geography. These are logical extensions of the hollow/filled-in arrows above, and merely add their features:

Double gravity: Represented by two filled-in gravity arrows pointing in the same direction, this hex causes the head of a ship's vector arrow to be pushed two hexes in the direction of the filled-in arrow for every hex passed through.


One-and-a-half gravity: Represented by one filled-in gravity arrow and one outlined gravity arrow pointing in the same direction, this hex causes the head of a ship's vector arrow to be pushed at least one hex in the direction of the filled-in arrow for every hex passed through, with every other hex of this type acting as a double gravity hex.


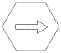Gravity arrows pointing at hex corners instead of hex sides: These mean that the direction of the gravity push is into either of the two hexes bordering the hex corner, at the player's discretion. This is most likely to occur with either objects that have a double ring of gravity hexes or binary objects. In most cases the gravity arrow will point directly at the object in question; the only likely exception to this rule is in some hexes between binary systems, where the effect of both gravity wells is to slingshot the ship between them; in these cases, there may be gravity wells pointing at an imaginary line connecting the two stellar objects.


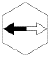Double-headed gravity arrows: Logically, this can only occur with two arrowheads of different strength (e.g., one outline and one filled-in), as same strength arrows would simply cancel each other out. This occurs when a two objects, one with a stronger gravity field, are in close proximity. This hex causes the head of a ship's vector arrow to be pushed at least one hex in the direction of the filled-in arrow for every hex passed through, with every other half-gravity hex causing a push in the opposite direction (thereby canceling the first arrow). Sometimes, therefore, this hex acts as a full-gravity hex, sometimes it acts as a no-gravity hex.


Double row of gravity hexes: Some types of stars and other objects with large gravity wells may have a second ring of half-gravity hexes surrounding an inner ring of double-gravity hexes. Note that in the outer ring, every other arrow will point at a hex corner instead of a hexside; all arrows should point directly at the stellar object generating the gravity well.